By Johnna Dukes, ABOC
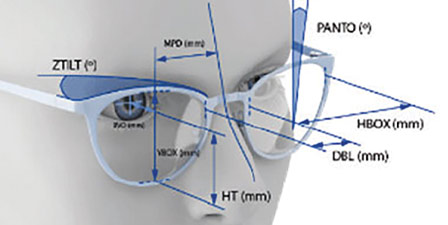
What’s the first thing you think about when you hear the words “wrap” and “pantoscopic tilt”? Wrapped sunglasses or athletic frames, yes? And while these types of frames do utilize both wrap and pantoscopic tilt, you actually come into contact with these angles all of the time in your day-to-day dispensing. Recognizing the effects of wrap and pantoscopic tilt will make you a better optician if you can become familiar with what happens optically when you encounter these conundrums not only when fitting wrapped sunwear or an athletic fitting frame, but also in your everyday fitting.
First, let’s consider what happens when you encounter wrapped lenses (Figure 1). Taking lenses from a flat front orientation and curving them around a vertical axis changes the placement of the optical center of the lens relative to the eye itself (or the pupillary axis). When lenses are wrapped around a vertical axis, what was a perpendicular relationship of the optical center of the lens and the pupil itself, now creates an optical center that is orientated more temporally than when the lens is mounted flat. When the optical center is wider than what is needed by the patient, this results in induced prismatic effect. In addition, it is difficult for the wearer to achieve good binocular vision when looking through a set of lenses which is inducing base out prism.
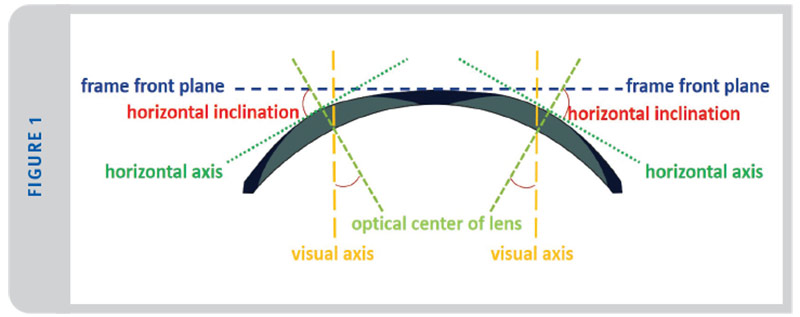
Next, because the direction of the wrap is the opposite in each lens (i.e., the left lens rotates counterclockwise, and the right lens rotates clockwise) there will be a resultant prismatic effect to the wearer. Prismatic effect due to wrap angle is not dependent on prescription, however, it is dependent on base curve, index of lens material, wrap angle and lens thickness. (Although the prescription of the lens will affect the thickness of the lens, therefore it does come into play to some degree.)
Induced Prism Calculator
Delta = 100 (t/n Cb Sin theta)
Delta is resultant prism
t=thickness
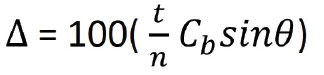
n=index of refraction
Cb=Base Curve
Sin theta = wrap angle
The use of this formula will demonstrate that just using a higher base curve lens and wrapping it around a vertical axis will create induced base out prism.
Let’s take the formula for a test drive. Imagine that the lens you’re working with is 4.0 mm thick. Index of refraction is 1.53, the base curve is 8, and the wrap angle is 20 degrees. First let’s change the thickness from millimeters to meters, changing the decimal point to .004. So, inserting the information we have: sin 20 x 8=2.736, .004/1.53 =0.0026 x2.736 =0.0071 x100 = 0.715, or .72 BO prism in each lens.
Consider that if your patient is looking through a lens that has an induced 0.72 diopter Base Out Prism in each lens, what are they likely going to remark about? “Pulling,” “discomfort,” “disorientation,” or “only being able to use one eye at a time” are all likely comments a dispenser would potentially hear from a patient who is experiencing issues like this, completely derived from looking through lenses that are mounted in a wrapped frame and uncompensated for the amount of prism would be induced for the wearer. Additionally, do you think this patient will be able to achieve binocular vision by use of these lenses?
Fortunately, a skilled optician (along with their skilled lab) can look at this situation and compensate the lens by ordering an equal amount of prism in the opposite direction in order to cancel the induced prism that occurs just by virtue of wrapping the lenses. However, the lab is not likely to run these compensations unless you, the skilled optician, can alert them to the need to compensate.
Pantoscopic tilt can create a similar and yet different situation considering that pantoscopic tilt happens when we rotate the lens on a horizontal axis making the bottom of the lens closer to the face and the top of the lens farther away from the face. While wrap angle creates opposing direction changes, pantoscopic tilt creates prism that would cancel as they are both the same direction (base down.) And remember that prism base down in equal amounts cancels each other out with a theoretical result being no prism. (Of course, we can discuss yolked prism, but that is another topic for another day.) What makes pantoscopic tilt different is the induction of oblique astigmatic power as found by Martin’s Formula. This formula shows us that adding more pantoscopic tilt will induce astigmatic power to the wearer.
(Martin’s formula)
New Sphere Power = D (1+sin2 a)/3
New Cylinder Power = D(tan2a)
Let’s take this formula for a spin. Let’s say we have a lens with a sphere power of -10.00 D, with 15 degrees of pantoscopic tilt. (a) so, 1+15 sin squared / 3 = 1.02; 1.02x10.00 = 10.22 D for the new sphere power.
Then, we have to find the new cylinder power, so we will take 15 tan squared =0.071 x10.00 =0.71, so the new cylinder power is 0.71D.
As a result, what was supposed to be a -10.00 sphere lens now is perceived by the patient at -10.22 -0.71 x 180. Do you think this patient will notice a difference in their vision? Again, by keeping in your back pocket the information that you now know about what happens when excessive pantoscopic tilt is applied to a lens, it can help you diagnose what a patient is experiencing when they remark that the lens they are wearing feels differently to them than a previous pair had.
Fortunately, we are dispensing in the 21st century, where we have access to freeform lens technology which allows labs to help us compensate for the need for base in prism to negate the resultant base out prism that occurs when using wrapped lenses. Freeform lenses also allow for point by point customization that can take into account incredibly difficult computations such as off-center refractive errors that occur when using part of the lens outside of the optical center. By identifying the proper measurements such as monocular PD, wrap angle and degrees of pantoscopic tilt, and providing this information along with the desired base curve and lens index, you, along with your lab, can truly create the computations that will be necessary to stave off the unwanted optical effects that exist when we do not take these items into account.
Creating a best case scenario for working with these types of frames is to truly look to your lab as your trusted teammate. You can look at these frames and determine that compensations will need to be made, and by speaking with your lab, they can recommend the proper materials, compensations and base curves that would be necessary in order to create best case scenarios in order to stave off the unwanted effects that wrap and pantoscopic tilt can have on the finished product.
Being able to look at wrap and pantoscopic tilt, and knowing what outcomes are likely to transpire from their presence allows you to better identify which problems you are likely to encounter by fitting wrapped frames, as well as help you identify these issues when you see them pop up in your everyday fitting. ■
Johnna Dukes is a board certified optician, ABO approved speaker and president of the Opticians Association of America.