This article is about how anti-reflection coating reduces reflections from eyeglass lenses. But before we go there let's ask a more fundamental question: Why does glass reflect in the first place, after all, isn't glass supposed to be transparent?
The answer is that the reflection isn't caused by the glass per se, but by the fact that the approaching light waves encounter a boundary where the index of refraction changes suddenly. Namely, the air-glass boundary where the index of refraction goes from nearly 1.0 (air) to about 1.5 (common glass). Whenever a wave—light wave, sound wave, water wave, waves on a rope, etc.—runs into a boundary where the conditions of propagation change, the wave doesn't ignore the change in conditions and continue on as though nothing happened. Instead it responds by dividing its energy between a transmitted wave that crosses the boundary and continues on, and a reflected wave that bounces back. In the case of glass with index 1.5, about 96 percent of the energy is transmitted and about 4 percent is reflected (for oblique angles of incidence these percentages are different). This link includes good animations of wave reflection and transmission at a boundary.
The laws of conservation of momentum and energy in physics demand the observed partial reflection/transmission behavior of a wave at a boundary. For example, if all the wave was transmitted at the boundary, the conservation of energy would be satisfied but the conservation of momentum would not, so some reflection has to occur so that both conservation laws are satisfied.
Since the boundary is responsible for reflection/transmission of the wave, it is the reasonable place to look for a way to reduce reflection. What if we were to manipulate the boundary so that the change in index is smooth instead of sudden? This actually works. Even though this is not the approach used in anti-reflection eyeglass lenses, the method is entertaining to mention because Nature uses it to reduce reflection in the eyes of some insects. See Figure 1.

Figure 1: The cone-like nano-structure on a moth's eye create a smooth transition zone between the index of refraction of air (about 1.0003 ) and the index of refraction of the optics of the moth's eye (I'm guessing, about 1.4). Source: phys.org
So far it has been impractical to use the moth-eye anti-reflection method to eyeglass lenses. It is expensive, not durable, vulnerable to contamination, and hard to clean. Instead, the reflection property of waves at a boundary is used to reduce reflection. Yes, the very property that causes the problem in the first place! The idea is to create a second reflected wave at the boundary that oscillates in the opposite way from the original reflected wave. When the original reflected wave is at its peak, the second reflected wave is at its valley and vice versa. In this way the two reflected waves cancel each other and all the energy goes into the transmitted wave. This phenomenon is known as phase cancellation. The best video I could find to illustrate phase cancellation deals with sound waves instead of light waves and also discusses cancellation in the audio context where it is undesirable. Nevertheless the video gives a good intuitive feel for what phase cancellation is. In any case the mathematics of phase cancellation is the same whether we are dealing with light waves, sound waves, water waves, waves on a rope, etc. Anti-reflection wave theory isn't just a subject in optics.
Here's the way eyeglass lenses are made anti-reflective. See Figure 2.
A thin layer of a transparent material with index of refraction in between air and the substrate (glass) is coated onto the glass. This creates two boundaries:
- Air-coating
- Coating-substrate
At each boundary there is a reflection. The thickness of the coating is chosen such that the waves reflected at the two boundaries cancel each other as they are reflected back out.
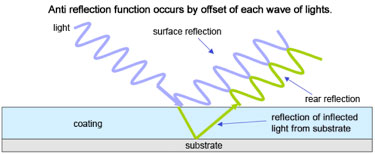
Figure 2. An anti-reflection coating is a thin layer of transparent material whose thickness is such that the reflection at the second boundary (bottom surface of coating where coating meets the substrate) cancels the reflection from the first boundary (top surface of coating where air meets coating) via the phase cancellation phenomenon. Note that the peaks of the first reflection (blue wave) lines up with the valleys of the second reflection (green wave). This is mathematically the same as adding a positive number to a negative number of the same magnitude. For example, 1+ (-1)=0. So there is now zero reflection from the surface. Even though the two waves are adding, they are adding with opposite phases resulting in zero energy being reflected.
Unfortunately it is not possible to choose a single coating thickness that creates phase cancellation for all wavelengths of light (colors) at the same time. The wavelength perfectly matching the coating thickness is cancelled entirely but the cancellation isn't as complete for the other wavelengths. This is why AR coated lenses reflect in color. The colors that you see in reflection are the ones less effectively cancelled. Even at the perfectly matching wavelength it is not possible to choose a single coating thickness that creates phase cancellation at all angles of incidence. Which is why the reflected color of an AR coated lens changes with angle. Both these shortcomings can be improved by using multi-layer coatings.
One last note before I end this brief intro to anti-reflection optics. For natural (unpolarized) light, the higher the index of refraction of the glass substrate, the more light is reflected at the boundary at all angles of incidence. A change in index from 1.52 (low index crown glass) to 1.67 (high index) increases reflectivity from about 4 percent to about 6 percent at zero degree incidence angle. So AR coating becomes more and more important as the glass index is increased. Fortunately, it turns out to be easier to use a single layer AR coating on higher index substrates because a coating material with an index of refraction between air and the substrate is easier to find (magnesium fluoride with index 1.37 is often used).
A first step into a technical understanding of coatings is familiarity with the reflection and transmission behavior of materials as a function of their index of refraction. Here's a web calculator where you can play with various indexes of refraction to see how much the material reflects and transmits at different angles.

Ari Siletz is president of CCDMETRIX. His company specializes in automated vision system inspection and metrology. With a background in both optical and software engineering, Ari has been developing instruments for the the ophthalmic and optical coating industries since the 1980s. Writing is one of Ari's serious hobbies. He is a published author whose short stories have appeared in numerous literary anthologies. He lives in Sebastopol, California.